Skip to main content

Linear Programming

Code​

Please visit this page for the code implementation of the LP method.

Formally, a linear program is an optimization problem of the form

minimize⁡  c⊤x subject to Ax=bx≥0,\begin{aligned} \operatorname{minimize} \; & \boldsymbol{c}^{\top} \boldsymbol{x} \\ \text { subject to } & \boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} \\ & \boldsymbol{x} \geq \mathbf{0}, \end{aligned}

where c∈Rn,b∈Rm\boldsymbol{c} \in \mathbb{R}^n, \boldsymbol{b} \in \mathbb{R}^m, and A∈Rm×n\boldsymbol{A} \in \mathbb{R}^{m \times n}. The vector inequality x≥0\boldsymbol{x} \geq \mathbf{0} means that each component of x\boldsymbol{x} is nonnegative. Several variations of this problem are possible; for example, instead of minimizing, we can maximize, or the constraints may be in the form of inequalities, such as Ax≥b\boldsymbol{A} \boldsymbol{x} \geq \boldsymbol{b} or Ax≤b\boldsymbol{A} \boldsymbol{x} \leq \boldsymbol{b}. 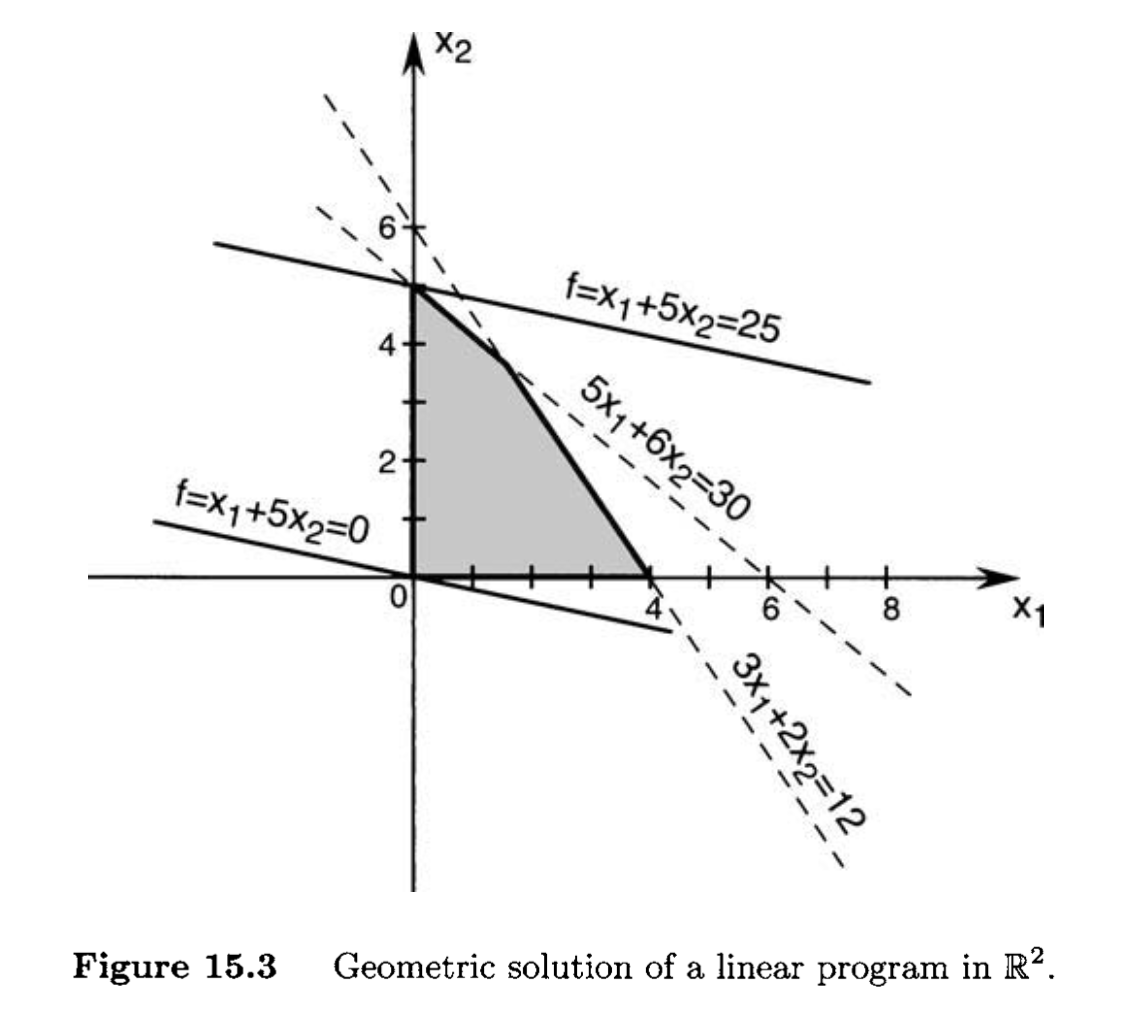Here A\boldsymbol{A} is an m×nm \times n matrix composed of real entries, m<n,rank⁡A=mm<n, \operatorname{rank} \boldsymbol{A}=m.

Standard Form Linear Programs​

If a linear program is in the form

minimize⁡  c⊤x subject to Ax≥bx≥0\begin{aligned} \operatorname{minimize} \; & \boldsymbol{c}^{\top} \boldsymbol{x} \\ \text { subject to } & \boldsymbol{A} \boldsymbol{x} \geq \boldsymbol{b} \\ & \boldsymbol{x} \geq \mathbf{0} \end{aligned}

then by introducing surplus variables yiy_i, we can convert the original problem into the standard form In more compact notation, the formulation above can be represented as minimize⁡c⊤x\operatorname{minimize} \boldsymbol{c}^{\top} \boldsymbol{x} subject to Ax−Imy=[A,−Im][xy]=b\boldsymbol{A} \boldsymbol{x}-\boldsymbol{I}_m \boldsymbol{y}=\left[\boldsymbol{A},-\boldsymbol{I}_m\right]\left[\begin{array}{l}\boldsymbol{x} \\ \boldsymbol{y}\end{array}\right]=\boldsymbol{b}

x≥0,y≥0,\boldsymbol{x} \geq \mathbf{0}, \boldsymbol{y} \geq \mathbf{0},

where Im\boldsymbol{I}_m is the m×mm \times m identity matrix. If, on the other hand, the constraints have the form

Ax≤bx≥0,\begin{aligned} \boldsymbol{A} \boldsymbol{x} & \leq \boldsymbol{b} \\ \boldsymbol{x} & \geq \mathbf{0}, \end{aligned}

then we introduce slack variables yiy_i to convert the constraints into the form

Ax+Imy=[A,Im][xy]=bx≥0,y≥0\begin{aligned} &\boldsymbol{A} \boldsymbol{x}+\boldsymbol{I}_m \boldsymbol{y}=\left[\boldsymbol{A}, \boldsymbol{I}_m\right]\left[\begin{array}{c} \boldsymbol{x} \\ \boldsymbol{y} \end{array}\right]=\boldsymbol{b} \\ &\boldsymbol{x} \geq \mathbf{0}, \boldsymbol{y} \geq \mathbf{0} \end{aligned}

where y\boldsymbol{y} is the vector of slack variables. Note that neither surplus nor slack variables contribute to the objective function c⊤x\boldsymbol{c}^{\top} \boldsymbol{x}.

In summary, to convert the problem into a standard form linear programming problem, we perform the following steps:

  1. Change the objective function to: minimize x1−x2x_1-x_2.
  2. Substitute x1=−x1′x_1=-x_1^{\prime}.
  3. Write ∣x2∣≤2\left|x_2\right| \leq 2 as x2≤2x_2 \leq 2 and −x2≤2-x_2 \leq 2.
  4. Introduce slack variables x3x_3 and x4x_4, and convert the inequalities above to x2+x3=2x_2+x_3=2 and −x2+x4=2-x_2+x_4=2.
  5. Write x2=u−v,u,v≥0x_2=u-v, u, v \geq 0.

Basic Solutions​

Definition​

We call [xB⊤,0⊤]⊤\left[\boldsymbol{x}_B^{\top}, \boldsymbol{0}^{\top}\right]^{\top} a basic solution to Ax=b\boldsymbol{A x}=\boldsymbol{b} with respect to the basis B\boldsymbol{B}. We refer to the components of the vector xB\boldsymbol{x}_B as basic variables and the columns of B\boldsymbol{B} as basic columns.

If some of the basic variables of a basic solution are zero, then the basic solution is said to be a degenerate basic solution. A vector x\boldsymbol{x} satisfying Ax=b,x≥0\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}, \boldsymbol{x} \geq \mathbf{0}, is said to be a feasible solution. A feasible solution that is also basic is called a basic feasible solution. If the basic feasible solution is a degenerate basic solution, then it is called a degenerate basic feasible solution.

Properties of Basic Solutions​

Definition​

Any vector x\boldsymbol{x} that yields the minimum value of the objective function c⊤x\boldsymbol{c}^{\top} \boldsymbol{x} over the set of vectors satisfying the constraints Ax=b,x≥0\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}, \boldsymbol{x} \geq \mathbf{0}, is said to be an optimal feasible solution.

An optimal feasible solution that is basic is said to be an optimal basic feasible solution.

Fundamental Theorem of LP​

Consider a linear program in standard form.

  1. If there exists a feasible solution, then there exists a basic feasible solution.
  2. If there exists an optimal feasible solution, then there exists an optimal basic feasible solution.

Proof​

We first prove part 1. Suppose that x=[x1,…,xn]⊤\boldsymbol{x}=\left[x_1, \ldots, x_n\right]^{\top} is a feasible solution and it has pp positive components. Without loss of generality, we can assume that the first pp components are positive, whereas the remaining components are zero. Then, in terms of the columns of A=[a1,…,ap,…,an]\boldsymbol{A}=\left[\boldsymbol{a}_1, \ldots, \boldsymbol{a}_p, \ldots, \boldsymbol{a}_n\right], this solution satisfies

x1a1+x2a2+⋯+xpap=b.x_1 \boldsymbol{a}_1+x_2 \boldsymbol{a}_2+\cdots+x_p \boldsymbol{a}_p=\boldsymbol{b} .

There are now two cases to consider.

Case 1: If a1,a2,…,ap\boldsymbol{a}_1, \boldsymbol{a}_2, \ldots, \boldsymbol{a}_p are linearly independent, then p≤mp \leq m. If p=mp=m, then the solution x\boldsymbol{x} is basic and the proof is done. If, on the other hand, p<mp<m, then, since rank⁡A=m\operatorname{rank} \boldsymbol{A}=m, we can find m−pm-p columns of A\boldsymbol{A} from the remaining n−pn-p columns so that the resulting set of mm columns forms a basis. Hence, the solution x\boldsymbol{x} is a (degenerate) basic feasible solution corresponding to the basis above.

Case 2: Assume that a1,a2,…,ap\boldsymbol{a}_1, \boldsymbol{a}_2, \ldots, \boldsymbol{a}_p are linearly dependent. Then, there exist numbers yi,i=1,…,py_i, i=1, \ldots, p, not all zero, such that

y1a1+y2a2+⋯+ypap=0.y_1 \boldsymbol{a}_1+y_2 \boldsymbol{a}_2+\cdots+y_p \boldsymbol{a}_p=\mathbf{0} .

We can assume that there exists at least one yiy_i that is positive, for if all the yiy_i are nonpositive, we can multiply the equation above by −1-1. Multiply the equation by a scalar ε\varepsilon and subtract the resulting equation from x1a1+x2a2+x_1 a_1+x_2 \boldsymbol{a}_2+ ⋯+xpap=b\cdots+x_p \boldsymbol{a}_p=\boldsymbol{b} to obtain

(x1−εy1)a1+(x2−εy2)a2+⋯+(xp−εyp)ap=b.\left(x_1-\varepsilon y_1\right) \boldsymbol{a}_1+\left(x_2-\varepsilon y_2\right) \boldsymbol{a}_2+\cdots+\left(x_p-\varepsilon y_p\right) \boldsymbol{a}_p=\boldsymbol{b} .

Let

y=[y1,…,yp,0,…,0]⊤\boldsymbol{y}=\left[y_1, \ldots, y_p, 0, \ldots, 0\right]^{\top}

Then, for any ε\varepsilon we can write

A[x−εy]=b.\boldsymbol{A}[\boldsymbol{x}-\varepsilon \boldsymbol{y}]=\boldsymbol{b} .

Let ε=min⁡{xi/yi:i=1,…,p,yi>0}\varepsilon=\min \left\{x_i / y_i: i=1, \ldots, p, y_i>0\right\}. Then, the first pp components of x−εy\boldsymbol{x}-\varepsilon \boldsymbol{y} are nonnegative, and at least one of these components is zero. We then have a feasible solution with at most p−1p-1 positive components. We can repeat this process until we get linearly independent columns of A\boldsymbol{A}, after which we are back to case 1 . Therefore, part 1 is proved.

We now prove part 2. Suppose that x=[x1,…,xn]⊤\boldsymbol{x}=\left[x_1, \ldots, x_n\right]^{\top} is an optimal feasible solution and only the first pp variables are nonzero. Then, we have two cases to consider. The first case is exactly the same as in part 1 . The second case follows the same arguments as in part 1 , but in addition we must show that x−εy\boldsymbol{x}-\varepsilon \boldsymbol{y} is optimal for any ε\varepsilon. We do this by showing that c⊤y=0\boldsymbol{c}^{\top} \boldsymbol{y}=0. To this end, assume that c⊤y≠0\boldsymbol{c}^{\top} \boldsymbol{y} \neq 0. Note that for ε\varepsilon of sufficiently small magnitude (∣ε∣≤min⁡{∣xi/yi∣:i=1,…,p,yi≠0})\left(|\varepsilon| \leq \min \left\{\left|x_i / y_i\right|: i=1, \ldots, p, y_i \neq 0\right\}\right), the vector x−εy\boldsymbol{x}-\varepsilon \boldsymbol{y} is feasible. We can choose ε\varepsilon such that c⊤x>c⊤x−εc⊤y=c⊤(x−εy)\boldsymbol{c}^{\top} \boldsymbol{x}>\boldsymbol{c}^{\top} \boldsymbol{x}-\varepsilon \boldsymbol{c}^{\top} \boldsymbol{y}=\boldsymbol{c}^{\top}(\boldsymbol{x}-\varepsilon \boldsymbol{y}). This contradicts the optimality of x\boldsymbol{x}. We can now use the procedure from part 1 to obtain an optimal basic feasible solution from a given optimal feasible solution.